Big O Notation and Complexity
Big O Notation helps us determine how complex an operation is. It's of particular interest to the field of Computer Science. So for all you CS geeks out there here's a recap on the subject!
When you start delving into algorithms and data structures you quickly come across Big O Notation. It tells us how long an operation will take to run, as the size of the data set increases.
It's also a measure of complexity. The simple fact is that if something takes longer to run it is obviously more complex... logical eh? :)
Big O Notation
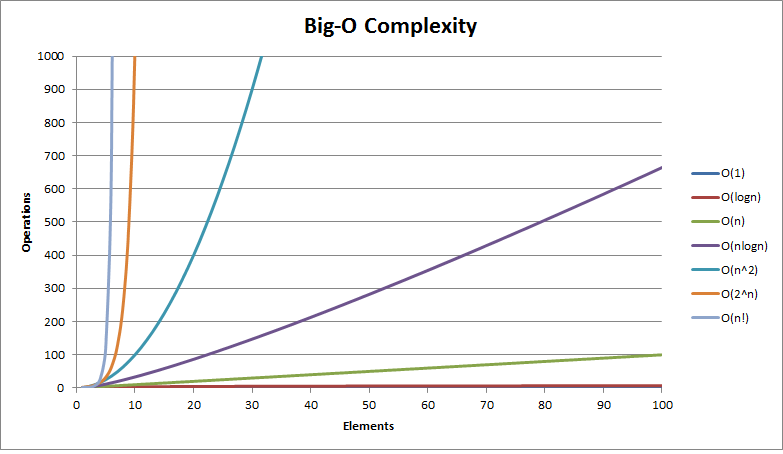
Here's a list of the more common Big O Notations from fastest (best) to slowest (worst).
| Notation | Description |
|---|---|
| O(1) | Constant: operations occur at the same speed no matter the size of the data set.
ie. doing a null check |
| O(log n) | Logarithmic: operations take slightly longer as the size of the data set increases in orders of magnitude. Very close to O(1).
ie. finding an item in a sorted data set using a binary search |
| O(n) | Linear: operations take longer in direct proportion to the size of the data set.
ie. adding up all the values in data set |
| O(n log n) | Linearithmic: as the data set doubles in size, operations take longer by an increasing multiplier of one.
ie. a quick sort |
| O(n2) | Quadratic: as the data set doubles in size, operations take four times longer.
ie. two nested loops over a data set |
| O(2n) | Exponential: for every new element added to the data set operations take twice as long.
ie. brute force attacking a password |
| O(n!) | Factorial: operations take n! times longer in direct proportion to the size of the data set.
ie. calculating fibonacci numbers recursively |
They say a picture is worth a thousand words so this should help greatly with your understanding of the above :)
Conclusion
The key take away here is that if you are working with large data sets you need to be very careful when selecting the data structure and/or algorithm you use.
I'm going to be starting a new series on Data Structures soon which will reference these Big O notations. That'll help show the real world application of these theoretical concepts.
Until then... happy coding!